船舶的倾斜角是多少?
横向静态稳性是指船舶在各种外部和内部因素的影响下保持直立的能力。我们知道,横向稳性只考虑横向或纵向的稳定性。
回到最基本的,当船舶受到来自横向的内部或外部干扰时,它往往会向某一侧倾斜或侧倾。同样,侧倾是由外力引起的倾斜,而侧倾是由于内部重量的转移。
倾斜度以倾斜角来衡量。分析初始完整稳定性时要考虑的最重要的点是重心 G、浮心 B 和稳心 M。在了解稳心时,重要的是要回顾稳定性的初始条件。
因此,当船舶倾斜时,稳心就是船舶中心线与通过浮心的线的交点。如果横向稳心垂直于重心上方,则船舶处于稳定或平衡状态。
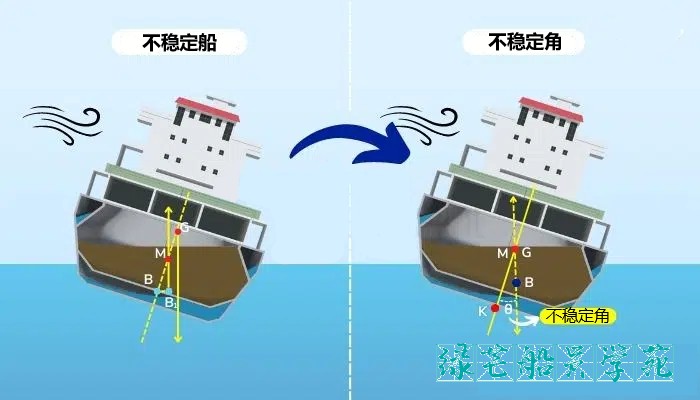
如果稳心与重心重合,则船舶处于中性状态。如果重心位于稳心之下,则船舶处于不稳定状态。当船舶倾斜时,复原杠杆或复原臂会通过其复原力矩将船舶拉回到直立位置。复原臂的长度直接决定了复原力矩。
目前,初始稳定性可分为两类研究:
1)大倾角稳定性
2)小倾角稳定性
在考虑小倾角时,通常将其视为 4 度或 5 度以内。但是,当侧倾或侧倾角大于半径的 4 度或 5 度时,则将其视为大倾角。
这是因为,从技术上讲,当倾角大于这个值时,M 不再是一个固定点,而是动态的。此外,它不再被视为稳定性的衡量标准,而是需要采用一些经过修改的、更为复杂的稳定性公式和计算方法。
因此,这些情况下复原力臂的确定需要特别考虑,可以使用 Atwood 公式或 Wall-sided 公式(Atwood 公式的一个特例)等关系式进行估算。我们不深入讨论公式和其他方面,因为它们超出了本文的讨论范围。
现在,对于大角度稳定性,出现了一个非常有趣的情况。正如我们从稳定性的第一原理中已经知道的那样,复原力臂或杠杆可以是正的、负的或零的。正复原力臂会产生正复原力矩,倾向于将船舶从不稳定位置带到直立位置。相反,负复原力矩会进一步推动船舶向侧面倾斜或侧倾。

对于零复原力臂,情况相当复杂。当稳心高度或 GM 为正或零时,力臂仍可为零,船舶处于平衡状态。此时,船舶应基本保持其位置,不会进一步倾斜,但同时不会趋向于恢复直立,因为没有力臂来产生所需的关键力矩。
尽管如此,由于正 GM,或者换句话说,正如我们所知,中心的位置位于重心上方,因此该船或多或少可以被视为“稳定”。但是,当船舶的复原力臂为零且 GM 为负时,可能会出现一种非常特殊的情况,不能被视为不稳定状态。在这种情况下,船舶将达到平衡状态,但永远不会达到平衡状态!听起来很奇怪,对吧?但在这种情况下确实如此。
由于 GM 为负,BM 为正,船舶永远不会倾覆,而会趋向于保持摆动状态,即来回摆动。船舶不会偏向任何一侧。在给定条件下,称为倾斜角,船舶处于连续横摇运动状态。
由于缺乏稳定的复原力臂,加上负 GM,船舶永远无法达到所需的稳定性或直立性。这也称为不稳定平衡状态。
不稳定是指船舶永远无法达到预期位置,平衡是指即使船舶无法达到预期位置,但船舶仍处于不会持续向一侧倾斜并倾覆的状态。然而,在这种不断振荡的状态下,如果由于某种原因甲板上进水,船舶可能会因增加的负载和力而倾覆。
在给定条件下,给定船舶的倾斜角可以通过 GM、稳心高度和 BM 以及稳心半径的值以数学方式确定。
按照GZ曲线,垂倾角出现在GZ或复原力臂为零并从负值转变为正值的拐点处。曲线上GZ为零的其他点是船舶处于自然直立状态,不受任何力的干扰,侧倾角为零,以及稳性曲线的末端,也称为消失稳性角。
在倾斜状态下,稳心高度或 GM 的大小是两倍,符号或方向相反。我们在本文中不进行详细计算。
这种持续的摇晃或摇摆状态对于乘客和船员来说非常危险。它可能会引发晕船、设备/系统损坏或货物和其他物品丢失等严重问题。
在恶劣天气条件下,海况已经受到干扰,船舶已经受到许多干扰,情况会进一步恶化。在这种情况下,船舶倾覆的可能性很大。从一开始,船倾角度就是设计师需要考虑的一个非常重要的问题。
大多数现代船舶都配有多种系统来抵消横摇运动,例如防摇水箱或其他防摇装置和机制。然而,出于实际目的,船舶始终小心避免这种倾斜度。
——END
- 发表于 2024-08-25 20:45
- 阅读 ( 1168 )
你可能感兴趣的文章
相关问题
0 条评论
文件生成中...
请稍候,系统正在生成您请求的文件

船舶的倾斜角是多少?

扫码过程中请勿刷新、关闭本页面,否则会导致支付失败
购买后请立即保管好,30天后需重新付费。

船舶的倾斜角是多少?

扫码过程中请勿刷新、关闭本页面,否则会导致支付失败
购买后请立即保管好,30天后需重新付费。
请点击下载或复制按钮进行操作
